
はじめに
この記事はTimee Product Advent Calendar 2025の23日目の記事です。
背景
営業やマーケティングの現場では、連続変数を特定のしきい値で区切って2値のKPIとして扱うケースがあります。例えば、「月の購入金額が1万円を超えた顧客を『ロイヤル顧客』と定義する」といったケースです。ここで、このKPIに対する施策の効果測定を行う際は、「ロイヤル顧客への転換率」をアウトカムに設定し、ABテストで群間の差を検定するのが最もシンプルなアプローチとして挙げられます。
連続的な現象を2値データとして観察した場合は、連続的な潜在変数および誤差項のモデリングと、閾値を基準とした2値化によって定式化できます。例えば、誤差項にロジスティック分布を仮定した場合にはロジットモデル(ロジスティック累積分布関数)に従います[1][2]。本ケースもこれと同様に考え、施策効果の分布の推定が可能です。ただし、ビジネス上の定義としてはわかりやすいこの2値化処理は、同時に本来持っていた情報を捨てることになり、効果測定における検出力が低下する(正規分布に従う変数を中央値でカットした場合、同じ検出力を得るためにはサンプルサイズが1.5倍必要[3])と報告されています。
このようなケースではもとの連続量も併せてモニタリングすることが推奨されますが、本稿では連続量のままモデリングする手法の有効性検証に焦点を当てます。 具体的には、2値化されたアウトカムを2値として扱う場合と、連続量分布を推定してから事後的にKPIを計算する場合とで、効果測定の正確さがどう変わるかを比較します。
実験
1.分布の仮定が正しい一回試行での比較
仮想のECサービスを考え、「売上が1万円以上」をロイヤル顧客とみなし、顧客のロイヤル率を改善する施策をABテストした状況を想定してサンプルデータを作成しました。
具体的には、「非購入者(0円)」と「購入者(対数正規分布に従う売上)」が混在する売上分布を仮定し、以下のパラメータp, μ, σのもと、各グループで500顧客分ずつ作成しました。
| パラメータ | Control | Treatment |
|---|---|---|
| 購入率 p | 0.50 | 0.53 |
| 対数平均 μ | 8.0 | 8.20 |
| 対数標準偏差 σ | 1.0 | 1.0 |
このとき、各サンプルデータが従う真の統計と施策効果は以下のようになります。
| 指標 | Control | Treatment | 効果 |
|---|---|---|---|
| 期待売上 | ¥2,457 | ¥3,182 | +¥724 |
| ロイヤル率 | 5.65% | 8.28% | +2.62pt |
次に、サンプルデータに対して以下の2つの手法でロイヤル顧客率に対する効果を推定し、真の施策効果を基準として比較しました。
- アウトカム2値化: 売上が1万円以上か否かのフラグを立て、その比率の差を直接比較する。
- アウトカム連続+ラベル事後計算: 真の尤度関数を用いて売上金額の分布を推定し、事後分布からロイヤル顧客の定義である「売上が1万円以上」を超える確率を計算して差を比較する。
2.分布の仮定が正しい複数回試行での比較
データが従う分布のパラメータを以下の範囲でランダムに変化させて作成しなおし、その他は1の設定を踏襲した実験を100回繰り返しました。そのうえで、2つの手法間で測定される効果の正確さを比較しました。
| 項目 | 値 |
|---|---|
| 購入率 p | 0.6〜0.8 |
| 購入率 p への効果 | +0.02〜+0.10 |
| 対数平均 μ | 7.9〜8.2 |
| 対数平均 μ への効果 | +0.05〜+0.20 |
| 対数標準偏差 σ | 0.7〜1.1 |
3.分布の仮定が誤っている複数回試行での比較
2.と同様の手順でサンプルデータを20回作成し、各データに対して3通りの尤度関数(対数正規分布・ガンマ分布・パレート分布)を用いた効果測定をそれぞれ実施しました。そのうえで、各尤度関数間で測定した効果の正確さを比較しました。
結果
1.分布の仮定が正しい一回試行での比較
2つの手法間での結果の差を図2に示します。
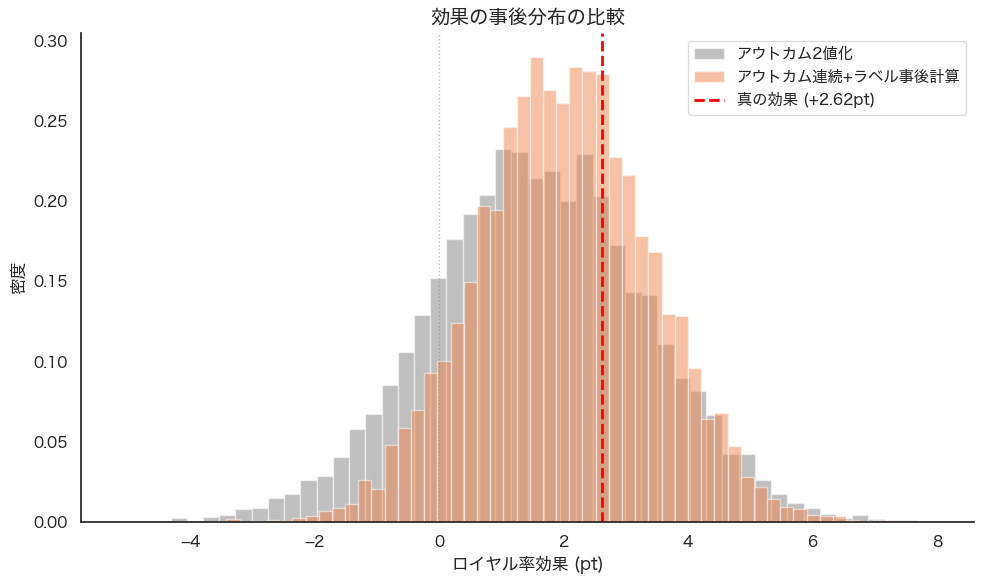
2つの手法はどちらも真の効果をほぼ捉えていますが、「アウトカム連続+ラベル事後計算」手法(グラフ橙色)は真の効果である+2.62pt付近に鋭い分布でピークがあり、真値に近い効果を比較的高い確信度で捉えました。
2.分布の仮定が正しい複数回試行での比較
2つの手法を繰り返したとき、測定した効果の真値に対する差の比較を図3に、分布の幅の広さの差を図4に示します。
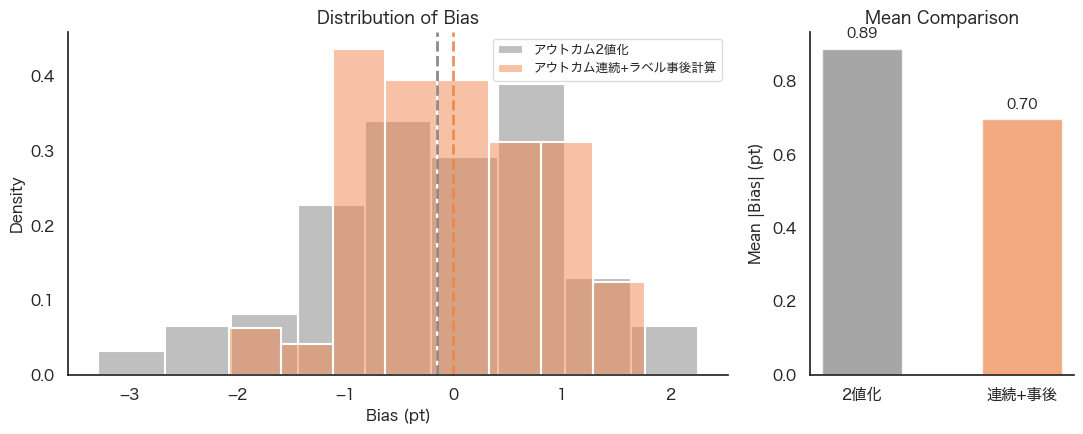
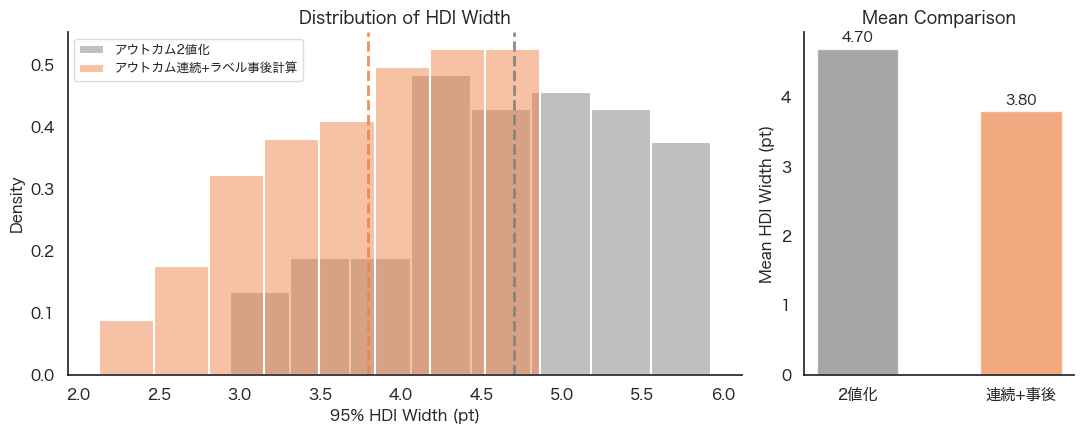
「アウトカム連続+ラベル事後計算」手法のほうが平均的に真値に近い効果を推定しました。
3.分布の仮定が誤っている複数回試行での比較
「アウトカム連続+ラベル事後計算」手法について、尤度関数を変えたとき測定した効果の真値に対する差の変化を図5に示します。
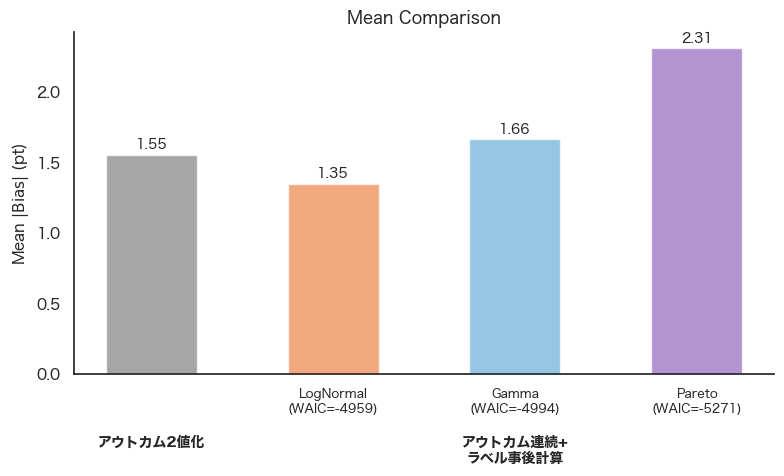
尤度関数として真の分布と異なる分布を仮定した場合、当てはまりが悪いほど測定した効果が真値から離れる傾向があり、いずれも「アウトカム2値化」手法と比較して正確さが悪化しました。
結論
- 連続量を2値化したKPIに対しては、Beta-Binomialモデルを用いた2値KPIに対する効果測定を、複雑な分布仮定を必要としないロバストなベースラインとして採用できます。
- より高い検出力を追求したい場合、連続量のまま分布をモデリングして効果測定し、事後分布からKPIを再計算するアプローチが有効な選択肢となりえます。 ただし誤った分布を仮定すると逆効果となるため、WAICによるモデル選定や閾値周辺の適合度の目視確認など、厳密なモデル選定が必要です。
参考文献
[1] Greene, W. H. (2003). Econometric Analysis (5th ed.), pp. 665-669.
[2] C. M. ビショップ (2007). パターン認識と機械学習 上 (元田 浩 他 訳).
[3] Cohen, J. (1983). The cost of dichotomization. Applied Psychological Measurement, 7(3).
おわりに
タイミーではデータ分析を通じてプロダクトの成長を支えるメンバーを募集しています。ご興味のある方はぜひお話ししましょう!